![next]()
![up]()
![previous]()
![contents]()
Next: Numeri naturali Up: Insiemi Previous: Costruzione e operazioni sugli Indice
Dati due insiemi  e
e 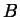 e degli elementi
e degli elementi 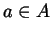 e
e 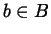 , sappiamo che è
possibile costruire l'insieme
, sappiamo che è
possibile costruire l'insieme 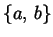 .
.
Se vogliamo
un insieme che ricordi che 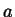 è da considerare
per primo e
è da considerare
per primo e 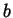 per secondo,
allora l'insieme
per secondo,
allora l'insieme 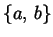 non va bene,
perché
non va bene,
perché 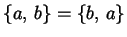 (hanno gli stessi
elementi). Per essere più precisi, vogliamo poter costruire per ogni
(hanno gli stessi
elementi). Per essere più precisi, vogliamo poter costruire per ogni 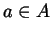 e
e 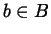 un insieme
un insieme 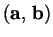 (che chiameremo coppia ordinata) in modo tale che si abbia:
(che chiameremo coppia ordinata) in modo tale che si abbia:
e tale che dalla coppia sia ricavabile il primo ed il secondo termine. Un
modo, per niente ovvio, è quello di porre la seguente:
Definizione 2.3.1 La
coppia ordinata con termini
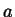
e
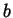
è l'insieme:
Definizione 2.3.2 L'insieme di tutte le possibili coppie con
primo termine in

e secondo termine
in
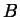
è chiamato
prodotto cartesiano di

e
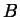
ed è indicato con:
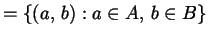
.
Esempio 2.3.3 Se
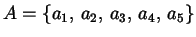
e
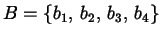
, il prodotto
cartesiano
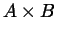
si può rappresentare con il rettangolo:
Possiamo addirittura omettere l'indicazione delle coppie e decidere, ad
esempio, che la casella all'incrocio di
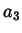
e
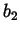
rappresenti la
coppia
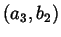
.
Una relazione tra gli elementi di  e gli elementi di
e gli elementi di 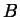 dal punto di vista
logico è un predicato di due variabili
dal punto di vista
logico è un predicato di due variabili 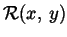 , in cui
, in cui 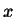 si fa variare solo
tra gli elementi di
si fa variare solo
tra gli elementi di  e
e 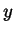 solo fra gli elementi di
solo fra gli elementi di 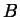 . Una relazione
logica
. Una relazione
logica 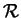 tra
tra  e
e 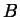 individua un sottoinsieme del prodotto cartesiano:
individua un sottoinsieme del prodotto cartesiano:
Esempio 2.3.4 Sia
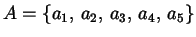
l'insieme delle aule di una facoltà e
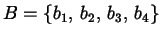
le ore di lezione
di una data mattina. Consideriamo la relazione
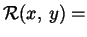
''l'aula
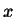
all'ora
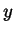
è occupata'', per
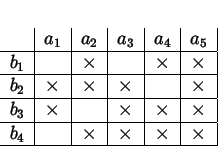
rappresentare tutte le possibili aule occupate alle varie ore. Possiamo usare
una tabella del tipo:
dove le caselle con la crocetta rappresentano le coppie
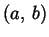
che verificano la
relazione, cioè tali che l'aula
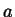
è occupata all'ora
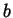
.
La relazione logica 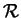 tra
tra  e
e 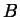 di solito ha un suo significato ed è definita mediante una ben precisa
costruzione simbolica, perciò contiene molta più informazione dell'insieme
di solito ha un suo significato ed è definita mediante una ben precisa
costruzione simbolica, perciò contiene molta più informazione dell'insieme 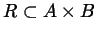 che si limita a
registrare quando
che si limita a
registrare quando 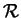 è verificata.
Tuttavia, se assumiamo il punto di vista che ciò che importa della relazione
è verificata.
Tuttavia, se assumiamo il punto di vista che ciò che importa della relazione
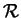 si riduce a ciò
che può dirci di vero o di falso sulle coppie
si riduce a ciò
che può dirci di vero o di falso sulle coppie 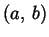 , allora
, allora 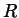 può sostituire
può sostituire
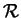 come relazione tra
come relazione tra
 e
e 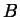 . Questa considerazione equivale ad affermare che due relazioni
. Questa considerazione equivale ad affermare che due relazioni 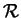 e
e 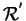 tra
tra  e
e 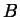 , che sono vere (false) nelle stesse coppie non sono distinguibili.
Questo è l'atteggiamento giusto per la teoria degli insiemi, che non suppone
l'esistenza a priori di relazioni matematiche, ma si propone di definirle come
insiemi, senza riceverle da altre teorie esterne. Viceversa, un qualunque
sottinsieme
, che sono vere (false) nelle stesse coppie non sono distinguibili.
Questo è l'atteggiamento giusto per la teoria degli insiemi, che non suppone
l'esistenza a priori di relazioni matematiche, ma si propone di definirle come
insiemi, senza riceverle da altre teorie esterne. Viceversa, un qualunque
sottinsieme 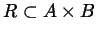 definisce una
relazione
definisce una
relazione 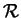 (magari senza un
particolare significato):
(magari senza un
particolare significato):
È per questo che poniamo la seguente
Definizione 2.3.5 Definiamo
relazione tra 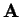 e
e 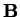
un qualunque
sottoinsieme
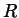
di
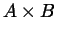
.
D'ora in poi, identificheremo 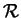 con
con 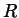 e quindi
scriveremo indifferentemente
e quindi
scriveremo indifferentemente 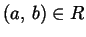 oppure
oppure 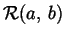 è vera;
scriveremo a volte anche
è vera;
scriveremo a volte anche 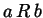 in luogo di
in luogo di 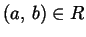 .
.
Definizione 2.3.6 Sia

un
insieme. Una relazione
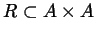
tra

e se stesso si dice
una
relazione di equivalenza se valgono le seguenti proprietà:
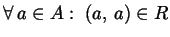 (proprietà
riflessiva);
(proprietà
riflessiva);
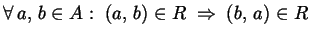 (proprietà simmetrica);
(proprietà simmetrica);
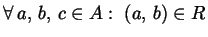 e
e 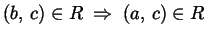 (proprietà
transitiva).
(proprietà
transitiva).
Quando si assegna una relazione di equivalenza 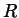 su un insieme
su un insieme  , l'insieme risulta
suddiviso in tanti sottoinsiemi:
, l'insieme risulta
suddiviso in tanti sottoinsiemi:
Definizione 2.3.9 Sia

un
insieme,
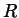
una relazione di
equivalenza su

ed
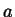
un elemento di

; si dice
classe
di equivalenza di
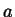
il seguente
sottoinsieme di

:
che raccoglie tutti gli elementi di

equivalenti all'elemento
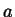
.
Definizione 2.3.11 Sia

un
insieme,
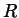
una relazione di
equivalenza su

. L'insieme di tutte
le classi di equivalenza di

(rispetto ad
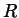
):
si dice
insieme quoziente di  (rispetto
ad
(rispetto
ad 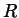 )
) e si indica
con
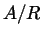
.
È possibile trovare un insieme 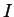 (insieme degli indici) ed associare ad ogni elemento
(insieme degli indici) ed associare ad ogni elemento 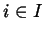 una classe di
equivalenza
una classe di
equivalenza 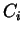 di
di  rispetto ad
rispetto ad 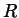 in modo tale che:
in modo tale che:
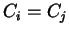 se e solo se
se e solo se
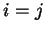 ;
;
- per ogni classe di equivalenza
![$C=[a]$](Prodotto cartesiano, relazioni_file/img147.gif) di
di
 rispetto ad
rispetto ad 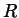 , esiste un
, esiste un 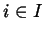 (ed uno solo)
tale che
(ed uno solo)
tale che 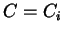 .
.
Allora
la famiglia di insiemi 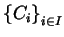 coincide con
coincide con 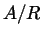 e verifica:
e verifica:
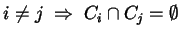 ;
;
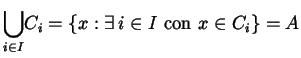 ;
;
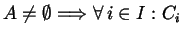 non è vuoto.
non è vuoto.
Definizione 2.3.12 Sia

un
insieme e
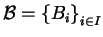
una famiglia di
sottoinsieme di

indicizzata
dall'insieme
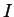
; diremo che
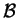
è una
partizione di 
se valgono le
seguenti proprietà:
- i
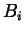 sono tutti non
vuoti se
sono tutti non
vuoti se  è non vuoto;
è non vuoto;
- i
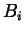 sono a due a
due disgiunti;
sono a due a
due disgiunti;
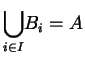 .
.
Una relazione 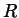 di equivalenza su
di equivalenza su
 definisce una
partizione di
definisce una
partizione di  nelle sue classi di
equivalenza; viceversa, data una partizione
nelle sue classi di
equivalenza; viceversa, data una partizione 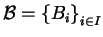 di
di  , è possibile
definire una relazione di equivalenza
, è possibile
definire una relazione di equivalenza 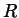 su
su  (indotta da
(indotta da 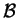 ) ponendo:
) ponendo:
Non è difficile verificare che la relazione 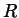 è effettivamente una relazione di equivalenza e che le sue classi di equivalenza
sono tutti e soli i sottoinsiemi
è effettivamente una relazione di equivalenza e che le sue classi di equivalenza
sono tutti e soli i sottoinsiemi 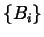 della partizione.
della partizione.
Inoltre la corrispondenza:
tra relazioni di equivalenza e partizioni è biunivoca, nel senso che :
- se
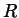 è una relazione
di equivalenza su
è una relazione
di equivalenza su  ,
, 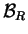 è la partizione
indotta da
è la partizione
indotta da 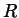 e
e 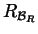 è la relazione definita da
è la relazione definita da 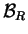 , allora
, allora 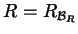 ;
;
- se
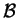 è una
partizione di
è una
partizione di  ,
, 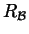 è la relazione definita da
è la relazione definita da 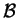 e
e 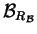 è la partizione
indotta da
è la partizione
indotta da 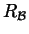 , allora
, allora 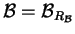 .
.
Esempio 2.3.13 Torniamo a considerare l'insieme:
con la relazione di equivalenza
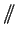
data dal parallelismo (d'ora in poi,
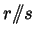
non escluderà
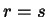
, anzi, per noi se
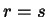
, allora
certamente si ha
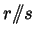
). Una classe di
equivalenza è costituita da tutte le rette parallele tra loro (o parallele ad
una retta assegnata). Possiamo dire che due rette sono nella stessa classe di
equivalenza se e solo se hanno la stessa direzione. Viceversa, se
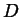
è l'insieme delle
''direzioni delle rette del piano'' e per ogni
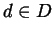
poniamo:
otteniamo una partizione
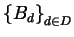
di

che coincide con la
partizione dovuta alla relazione di equivalenza data dal parallelismo.
Nell'esempio precedente si suppone di sapere già che cosa è la direzione
di una retta e di saper decidere se due rette hanno la stessa direzione.
Possiamo decidere, invece, di non sapere cosa sono le direzioni e decidere di
''inventarle'' affermando che le ''direzioni'' sono le classi di
equivalenza di rette parallele. In questo modo una ''direzione'' viene ad essere
un insieme ed anche se questo risulta innaturale è però molto vantaggioso.
La relazione che afferma che 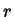 ed
ed 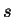 hanno la stessa
direzione diventa allora la relazione:
hanno la stessa
direzione diventa allora la relazione: 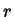 ed
ed 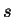 stanno nello
stesso insieme ''direzione''.
stanno nello
stesso insieme ''direzione''.
Esempio 2.3.14 Sia
![$A=[0,\, 1]$](Prodotto cartesiano, relazioni_file/img176.gif)
l'intervallo chiuso dei numeri reali tra
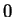
e
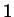
; se vogliamo
costruire un nuovo insieme in cui i numeri
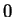
ed
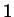
, e solo loro,
siano identificati, possiamo ricorrere alla relazione di equivalenza così
definita:
A questa relazione corrisponde la seguente partizione:
e quindi l'insieme quoziente
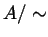
ha
tanti elementi quanti sono i numeri
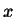
in
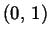
, e in più ha
l'elemento
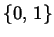
che rappresenta
l'elemento ottenuto ''
incollando''
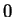
e
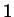
.
Definizione 2.3.15 Sia

un
insieme ed
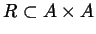
una relazione tra
gli elementi di

; si dice che
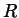
è una
relazione
d'ordine (
debole o parziale) se verifica le seguenti proprietà:
- OD1)
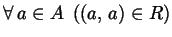 (proprietà riflessiva);
(proprietà riflessiva);
- OD2)
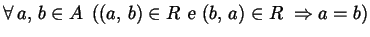 (proprietà antisimmetrica);
(proprietà antisimmetrica);
- OD3)
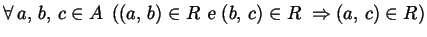 (proprietà transitiva).
(proprietà transitiva).
Osservazione 2.3.16 Se indichiamo
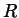
con il simbolo
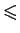
e scriviamo
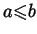
invece di
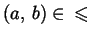
, le tre proprietà
date sopra acquistano la seguente forma:
- OD1)
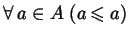 ;
;
- OD2)
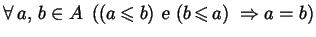 ;
;
- OD3)
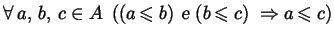 .
.
Il simbolo
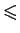
si
legge ''
minore o uguale'' come per l'ordinamento naturale dei numeri
reali, ma può non avere niente a che fare con l'ordinamento naturale, persino
nel caso in cui

sia
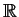
o un suo
sottoinsieme.
Definizione 2.3.17 Sia

un
insieme e
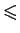
un ordinamento
(debole) su

. L'ordinamento
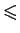
si dice
totale se vale inoltre la proprietà:
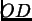
4)
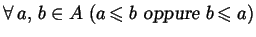
.
Definizione 2.3.18 Sia

un
insieme e
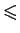
un ordinamento
debole su

. La relazione così
definita:
si dice l'
ordinamento stretto definito da
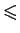
.
Osservazione 2.3.19 L'ordinamento stretto
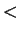
verifica le
seguenti due proprietà:
- OS1)
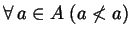 ;
;
- OS2)
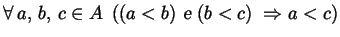 .
.
Osservazione 2.3.21 La corrispondenza tra ordinamenti deboli
e stretti su

:
è biunivoca e cosìla corrispondenza:
Definizione 2.3.22 Sia

un
insieme e
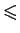
un ordinamento
totale su

. Un elemento
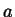
si dice un
minimo di

se:
si dice un
massimo di

se:
Osservazione 2.3.23 Un insieme

con un ordinamento
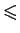
può non avere né
massimo né minimo, ma se ha un massimo (o un minimo) questo è unico e possiamo
indicarli con:
Definizione 2.3.24 Sia

un
insieme e
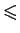
un ordinamento
debole su

. Un elemento
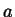
di

si dice un
elemento minimale di

se:
si dice un
elemento massimale di

se:
Osservazione 2.3.25 
- Un minimo (massimo) è un elemento minimale (massimale); in generale non è
vero il viceversa;
- un insieme con un ordinamento debole può avere diversi elementi minimali e
diversi elementi massimali.
Esempio 2.3.26 Sia

l'insieme
dei ''
punti della lettera 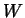
'', ordinati
nel modo seguente:
Questo insieme ha due elementi minimali e quattro elementi massimali,
nessun minimo e nessun massimo.
Definizione 2.3.27 Se

è un
insieme con un ordinamento
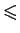
e
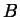
è un sottoinsieme
di

, allora gli
elementi di
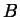
ricevono un
ordinamento dall'ordinamento di

(
ordinamento
indotto da  con
con 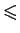 su
su 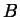
).
In termini di insiemi, l'ordinamento indotto è l'insieme:
Un sottonisieme 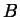 di
di  può avere elementi
minimi, massimi, minimali o massimali indipendentemente da
può avere elementi
minimi, massimi, minimali o massimali indipendentemente da  .
.
Definizione 2.3.28 Un insieme

con un ordinamento
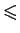
si dice
bene
ordinato se ogni suo sottoinsieme non vuoto ha minimo.
Esempio 2.3.29 
- Si può dimostrare (ma non è per niente facile) che
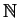 con
l'ordinamento naturale è bene ordinato;
con
l'ordinamento naturale è bene ordinato;
- L'insieme
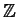 degli interi
con l'ordinamento naturale non è bene ordinato;
degli interi
con l'ordinamento naturale non è bene ordinato;
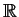 con
l'ordinamento naturale non è bene ordinato;
con
l'ordinamento naturale non è bene ordinato;
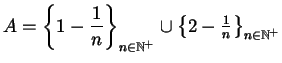 con l'ordinamento indotto da
con l'ordinamento indotto da 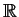 è bene ordinato;
è bene ordinato;
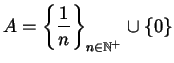 con l'ordinamento indotto da
con l'ordinamento indotto da 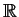 non è bene ordinato;
non è bene ordinato;
Definizione 2.3.31 Sia

un
insieme con un buon ordinamento
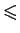
; per
ogni elemento
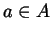
(che non sia
l'eventuale massimo di

) chiameremo
successivo di 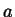 in
in 
l'elemento:
Esempio 2.3.32 
- In
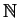 (con
l'ordinamento naturale) il successivo di ogni
(con
l'ordinamento naturale) il successivo di ogni 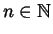 è
dato dall'elemento
è
dato dall'elemento 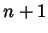 ;
;
- la nozione di successivo di un elemento è definibile anche in
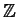 (con
l'ordinamento naturale), pur non essendo
(con
l'ordinamento naturale), pur non essendo 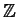 bene ordinato;
bene ordinato;
- In
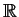 (con
l'ordinamento naturale) non è definibile il successivo di alcun elemento.
(con
l'ordinamento naturale) non è definibile il successivo di alcun elemento.
![next]()
![up]()
![previous]()
![contents]()
Next: Numeri naturali Up: Insiemi Previous: Costruzione e operazioni sugli Indice
Antonio Cassa
2000-04-14 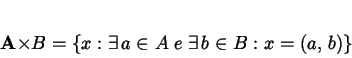
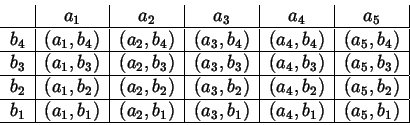
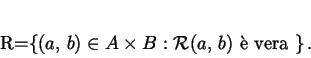
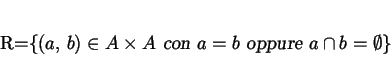
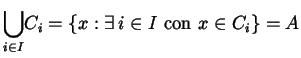 ;
;
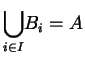 .
. 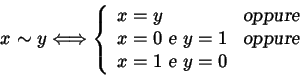
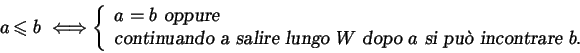
![\includegraphics [width=3.0cm]{wu.eps}](Prodotto cartesiano, relazioni_file/img213.gif)
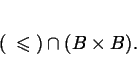
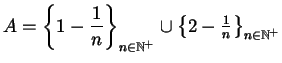 con l'ordinamento indotto da
con l'ordinamento indotto da 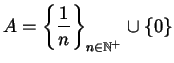 con l'ordinamento indotto da
con l'ordinamento indotto da